Python DataStructure
算法分析
列表
性能分析
append方法 O(1)
拼接运算符 O(k)
def test1():
l = []
for i in range(1000):
l += [i]
def test2():
l = []
for i in range(1000):
l.append(i)
def test3():
l = [i for i in range(1000)]
def test4():
l = list(range(1000))
测试:
tx = Timer('testx()', 'from __main__ import testx')
print('testx:', tx.timeit(number=10000))
结果:
test1: 1.2933769000000002
test2: 1.3480031999999997
test3: 0.5096997000000001
test4: 0.12439420000000023
| 操作 | 时间复杂度 |
|---|---|
| index[] | O(1) |
| index assignment | O(1) |
| append | O(1) |
| pop() | O(1) |
| pop(i) | O(n) |
| insert(i, item) | O(n) |
| del operator | O(n) |
| iteration | O(n) |
| contains (in) | O(n) |
| get slice [x:y] | O(k) |
| del slice | O(n) |
| set slice | O(n+k) |
| reverse | O(n) |
| concatenate | O(k) |
| sort | O(n log n) |
| multiply | O(nk) |
字典
性能分析
| 操作 | 时间复杂度 |
|---|---|
| copy | O(n) |
| get item | O(1) |
| set item | O(1) |
| delete item | O(1) |
| contains (in) | O(1) |
| iteration | O(n) |
数据结构
栈
特点:LIFO 后进先出
栈的常用操作:
Stack()创建空的新栈push(item)把一个新项添加到栈顶pop()从栈中删除顶部,返回itempeek()从栈中获取顶部,但不会删除isEmpty()测试栈是否空,返回布尔值size()返回栈中的 item 数量,返回整数
栈的实现
class Stack:
def __init__(self):
self.items = []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[-1]
def isEmpty(self):
return not self.items
def size(self):
return len(self.items
十进制、二进制转换
def divideBy2(num):
rem_stack = Stack()
while num != 0:
rem_stack.push(num % 2)
num //= 2
res = ''
while not rem_stack.isEmpty():
res += str(rem_stack.pop())
return res
前中后缀
中缀转后缀
def infix_to_postfix(infixexpr):
prec = {}
prec['*'] = 3
prec['/'] = 3
prec['+'] = 2
prec['-'] = 2
prec['('] = 1
opstack = Stack()
res = ''
expr = infixexpr.replace(' ', '')
for n in expr:
if n in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or n in "0123456789":
res += n
elif n == '(':
opstack.push(n)
elif n == ')':
top = opstack.pop()
while top != '(':
res += top
top = opstack.pop()
else:
# 如果当前遇到的操作符优先级小于之前放的操作符,先把之前的操作符弹出
while (not opstack.isEmpty() and prec[opstack.peek()] >= prec[n]):
res += opstack.pop()
opstack.push(n)
while not opstack.isEmpty():
res += opstack.pop()
return res
队列
特点:FIFO,先进先出
队列常用操作
Queue()创建空的新队列enqueue(item)把新项添加到队尾dequeue()从队首移除项isEmpty()查看队列是否空,返回布尔值size()返回队列的项数,返回一个整数
队列的实现
烫手山芋
队列轮流报数,报到对应num数则淘汰
def hot_potato(namelist, num):
q = Queue()
for name in namelist:
q.enqueue(name)
while q.size() != 1:
for _ in range(num - 1):
q.enqueue(q.dequeue())
q.dequeque()
return q.dequeue()
模拟打印机
打印机有两种模式:草稿模式 - 每分钟10页, 高质量模式 - 每分钟5页,要看哪种模式能完成更多的任务
10名学生,每个学生打印两次,任务长度1-20页
建模: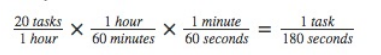
可以随机180秒有可能有一个任务发生
优先队列(堆)
特殊的队列(有“插队”现象),优先的值可以排在前面,优先出列。一般采用二叉堆。
性质:
- 是个完全二叉树 —— 堆是除了底层外都被填满的二叉树,底层节点从左向右填入。
- 小顶堆(Min-Heap)——任意父节点都比它的子节点要小;大顶堆(Max-Heap)则相反
基本的堆操作
-
插入
为了可以插入元素 x ,需要从底部向上查找可以插入的坑位,否则将其父节点向下移动。直到找到可以插入的位置。
-
弹出堆顶